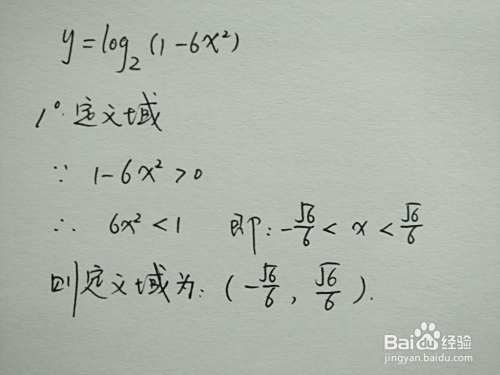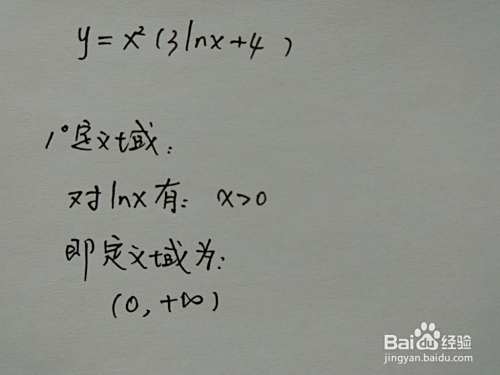形如∫dx/(ψ-φx)不定积分的计算

本例为微积分不定积分计算，积分函数为一次函数倒数形式，并列举当系数均为整数情形、为根式情形和分数情况等不同情况下计算详细过程。

方法/步骤

1、通用步骤推导：

∫dx/(ψ-φx)=-∫dx/(φx-ψ)

=-(1/φ)∫dφx/(φx-ψ)

=-(1/φ)∫d(φx-ψ)/(φx-ψ)

=-(1/φ)ln|φx-ψ|+C。

2、当系数均为整数情形

1.当ψ=1，φ=1情形：

∫dx/(1-x)=-∫dx/(x-1)=-∫d(x-1)/(x-1)=-ln|x-1|+C。

3、2.当ψ=1，φ=388情形：

∫dx/(1-388x)=-∫dx/(388x-1)=-(1/388)∫d388x/(388x-1)

=-(1/388)∫d(388x-1)/(388x-1)=-(1/388)ln|388x-1|+C。

4、3.当ψ=176，φ=1情形：

∫dx/(176-x)=-∫dx/(x-176)=-∫d(x-176)/(x-176)=-ln|x-176|+C。

5、4.当ψ=364，φ=335情形：

∫dx/(364-335x)=-∫dx/(335x-364)

=-(1/335)∫d335x/(335x-364)

=-(1/335)∫d(335x-364)/(335x-364)

=-(1/335)ln|335x-364|+C。

6、当两个系数均为根式情形

1.当ψ=√179，φ=√131情形：

∫dx/(√179-√131x)=-∫dx/(√131x-√179)

=-(1/√131)∫d√131x/(√131x-√179)

=-(1/√131)∫d(√131x-√179)/(√131x-√179)

=-(1/√131)ln|√131x-√179|+C。

7、2.当ψ=√308，φ=√908情形：

∫dx/(√308-√908x)=-∫dx/(2√227x-2√77)

=-(1/2√227)∫d2√227x/(√131x-2√77)

=-(1/2√227)∫d(2√227x-2√77)/(2√227x-2√77))

=-(1/2√227)ln|2√227x-2√77|+C。

8、当系数均为分数情况：

当ψ=3/20√308，φ=5/47情形：

∫dx/(3/20-5x/47)

=-∫dx/(5x/47-3/20)

=-(47/5)∫d(5x/47)/(5x/47-3/20)

=-(47/5)∫d(5x/47-3/20)/(5x/47-3/20)

=-(47/5)ln|5x/47-3/20|+C。

本文来自于百度作者：吉禄学阁，仅代表原作者个人观点。本站旨在传播优质文章，无商业用途。如不想在本站展示可联系删除