高中数学梯形图题目常见类型有哪些？

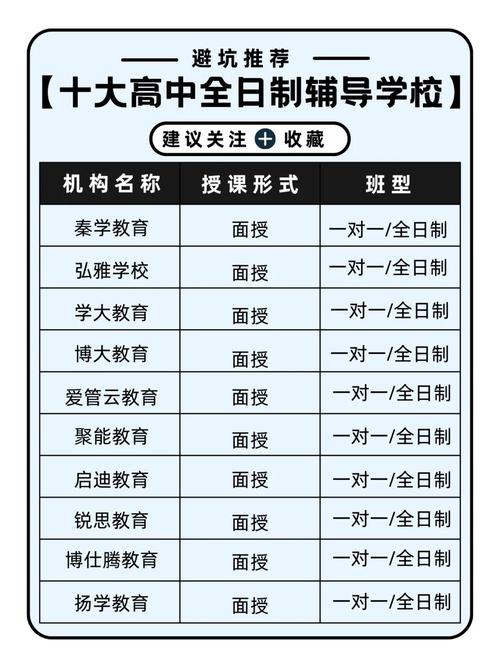
梯形是平面几何中常见图形之一，在高考数学、日常练习中常以不同形式出现，以下整理高中数学涉及梯形图的核心题型及解题思路，帮助学生掌握解题逻辑。

一、基础题型：梯形周长与面积计算

已知梯形ABCD中，AD∥BC，AD=8cm，BC=12cm，高为5cm，求：

1、梯形面积

解析：直接套用面积公式

S=(AD+BC)×h÷2=(8+12)×5÷2=50cm²

2、若腰AB=6cm，求梯形周长

解析：周长=上底+下底+两腰=8+12+6×2=32cm

关键点：区分梯形底边与腰的关系，明确公式中各参数含义

二、进阶题型：含特殊角的梯形计算

直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，BC=6，AD=3，求：

1、对角线AC的长度

解析：构造直角三角形ABC，使用勾股定理

AC=√(AB²+BC²)=√(16+36)=√52=2√13

2、梯形内角∠ADC的度数

解析：过D作DH⊥BC于H，CH=BC-AD=3，DH=AB=4

tan∠ADC=DH/CH=4/3 → ∠ADC≈53.13°

技巧提示：遇到直角梯形优先考虑构造辅助垂线

三、坐标系中的梯形证明题

已知四点A(0,0)、B(2,4)、C(6,4)、D(8,0)，判断是否为梯形并说明类型。

解题步骤：

1、计算各边斜率：k_AB=2，k_BC=0，k_CD=-1，k_DA=0

2、观察平行边：AD与BC斜率均为0，AB斜率2与CD斜率-1不相等

3、梯形（仅有一组对边平行），属于直角梯形（存在水平边）

易错提醒：验证平行条件时需严格比对斜率

四、动态几何综合题

等腰梯形ABCD中，AD∥BC，AB=CD=5cm，AD=6cm，BC=10cm，点P从A出发沿AD移动，速度为1cm/s，同时点Q从C出发沿CB移动，速度2cm/s，求t秒后梯形APQD与梯形PQBC的面积比。

分析过程：

1、建立时间变量t，确定AP=6-t，CQ=10-2t

2、推导PQ位置关系，建立面积表达式

3、联立方程求解临界点，注意0≤t≤5（Q点移动限制）

核心方法：动态问题需建立时间与线段的函数关系

个人观点

梯形题目训练能培养空间想象与代数转化能力，建议重点掌握以下三点：

1、熟练绘制梯形辅助线（高线、对角线、平移腰）

2、建立坐标系处理复杂位置关系

3、将几何条件转化为方程的能力

每日保持2-3题的练习量，配合错题归纳，可显著提升解题速度。